About
Shapes
Unary Geometric Queries
Binary Functions
Dynamic Tree
Broad-Phase

About

The Collision module contains shapes and functions that operate on them. The module also contains a dynamic tree and broad-phase to acceleration collision processing of large systems.

The collision module is designed to be usable outside of the dynamic system. For example, you can use the dynamic tree for other aspects of your game besides physics.

However, the main purpose of LiquidFun is to provide a rigid body physics engine, so the using the collision module by itself may feel limited for some applications. Likewise, I will not make a strong effort to document it or polish the APIs.

Shapes

Shapes describe collision geometry and may be used independently of physics simulation. At a minimum, you should understand how to create shapes that can be later attached to rigid bodies.

LiquidFun shapes implement the b2Shape base class. The base class defines functions to:

• Test a point for overlap with the shape.
• Perform a ray cast against the shape.
• Compute the shape's AABB.
• Compute the mass properties of the shape.

In addition, each shape has a type member and a radius. The radius even applies to polygons, as discussed below.

Keep in mind that a shape does not know about bodies and stand apart from the dynamics system. Shapes are stored in a compact form that is optimized for size and performance. As such, shapes are not easily moved around. You have to manually set the shape vertex positions to move a shape. However, when a shape is attached to a body using a fixture, the shapes move rigidly with the host body. In summary:

• When a shape is not attached to a body, you can view it’s vertices as being expressed in world-space.
• When a shape is attached to a body, you can view it’s vertices as being expressed in local coordinates.

Circle Shapes

Circle shapes have a position and radius. Circles are solid. You cannot make a hollow circle using the circle shape.

   b2CircleShape circle;
   circle.m_p.Set(2.0f, 3.0f);
   circle.m_radius = 0.5f;

Polygon Shapes

Polygon shapes are solid convex polygons. A polygon is convex when all line segments connecting two points in the interior do not cross any edge of the polygon. Polygons are solid and never hollow. A polygon must have 3 or more vertices.

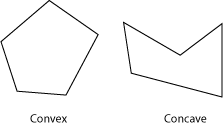
Polygon vertices are stored with a counter clockwise winding (CCW). We must be careful because the notion of CCW is with respect to a right-handed coordinate system with the z-axis pointing out of the plane. This might turn out to be clockwise on your screen, depending on your coordinate system conventions.

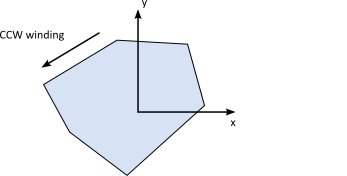
The polygon members are public, but you should use initialization functions to create a polygon. The initialization functions create normal vectors and perform validation.

You can create a polygon shape by passing in a vertex array. The maximal size of the array is controlled by b2_maxPolygonVertices which has a default value of 8. This is sufficient to describe most convex polygons.

The b2PolygonShape::Set function automatically computes the convex hull and establishes the proper winding order. This function is fast when the number of vertices is low. If you increase b2_maxPolygonVertices, then the convex hull computation might become slow. Also note that the convex hull function may eliminate and/or re-order the points you provide.

   // This defines a triangle in CCW order.
   b2Vec2 vertices[3];
   vertices[0].Set(0.0f, 0.0f);
   vertices[1].Set(1.0f, 0.0f);
   vertices[2].Set(0.0f, 1.0f);
   int32 count = 3;
   b2PolygonShape polygon;
   polygon.Set(vertices, count);

The polygon shape has some convenience functions to create boxes.

   void SetAsBox(float32 hx, float32 hy);
   void SetAsBox(float32 hx, float32 hy, const b2Vec2& center, float32 angle);

Polygons inherit a radius from b2Shape. The radius creates a skin around the polygon. The skin is used in stacking scenarios to keep polygons slightly separated. This allows continuous collision to work against the core polygon.

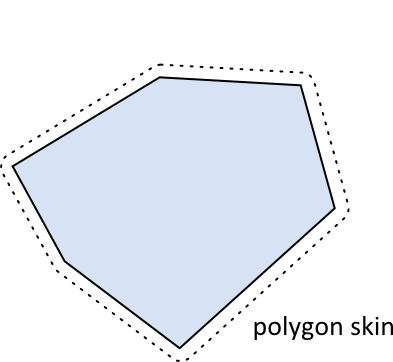
The polygon skin helps prevent tunneling by keeping the polygons separated. This results in small gaps between the shapes. Your visual representation can be larger than the polygon to hide any gaps.

Edge Shapes

Edge shapes are line segments. These are provided to assist in making a free-form static environment for your game. A major limitation of edge shapes is that they can collide with circles and polygons but not with themselves. The collision algorithms used by LiquidFun require that at least one of two colliding shapes have volume. Edge shapes have no volume, so edge-edge collision is not possible.

   // This an edge shape.
   b2Vec2 v1(0.0f, 0.0f);
   b2Vec2 v2(1.0f, 0.0f);
   b2EdgeShape edge;
   edge.Set(v1, v2);

In many cases a game environment is constructed by connecting several edge shapes end-to-end. This can give rise to an unexpected artifact when a polygon slides along the chain of edges. In the figure below we see a box colliding with an internal vertex. These ghost collisions are caused when the polygon collides with an internal vertex generating an internal collision normal.

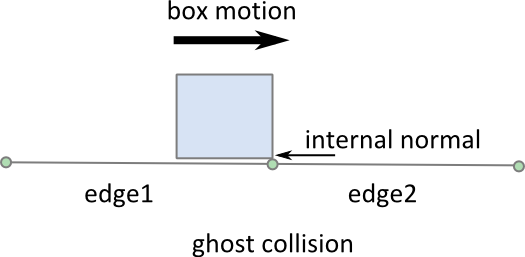
If edge1 did not exist this collision would seem fine. With edge1 present, the internal collision seems like a bug. But normally when LiquidFun collides two shapes, it views them in isolation.

Fortunately, the edge shape provides a mechanism for eliminating ghost collisions by storing the adjacent *ghost *vertices. LiquidFun uses these ghost vertices to prevent internal collisions.

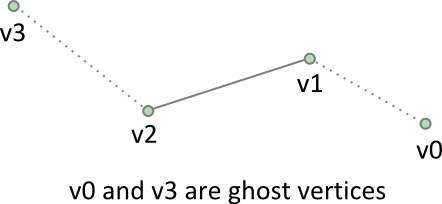
   // This is an edge shape with ghost vertices.
   b2Vec2 v0(1.7f, 0.0f);
   b2Vec2 v1(1.0f, 0.25f);
   b2Vec2 v2(0.0f, 0.0f);
   b2Vec2 v3(-1.7f, 0.4f);
   b2EdgeShape edge;
   edge.Set(v1, v2);
   edge.m_hasVertex0 = true;
   edge.m_hasVertex3 = true;
   edge.m_vertex0 = v0;
   edge.m_vertex3 = v3;

In general stitching edges together this way is a bit wasteful and tedious. This brings us to chain shapes.

Chain Shapes

The chain shape provides an efficient way to connect many edges together to construct your static game worlds. Chain shapes automatically eliminate ghost collisions and provide two-sided collision.

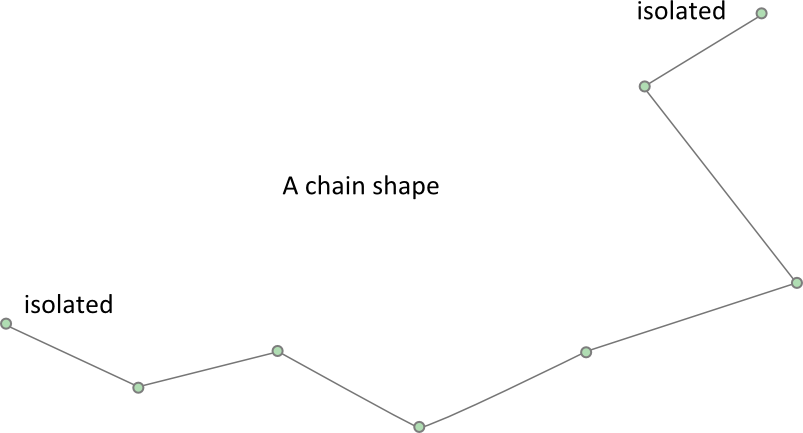
   // This a chain shape with isolated vertices
   b2Vec2 vs[4];
   vs[0].Set(1.7f, 0.0f);
   vs[1].Set(1.0f, 0.25f);
   vs[2].Set(0.0f, 0.0f);
   vs[3].Set(-1.7f, 0.4f);
   b2ChainShape chain;
   chain.CreateChain(vs, 4);

You may have a scrolling game world and would like to connect several chains together. You can connect chains together using ghost vertices, like we did with b2EdgeShape.

   // Install ghost vertices
   chain.SetPrevVertex(b2Vec2(3.0f, 1.0f));
   chain.SetNextVertex(b2Vec2(-2.0f, 0.0f));

You may also create loops automatically.

   // Create a loop. The first and last vertices are connected.
   b2ChainShape chain;
   chain.CreateLoop(vs, 4);

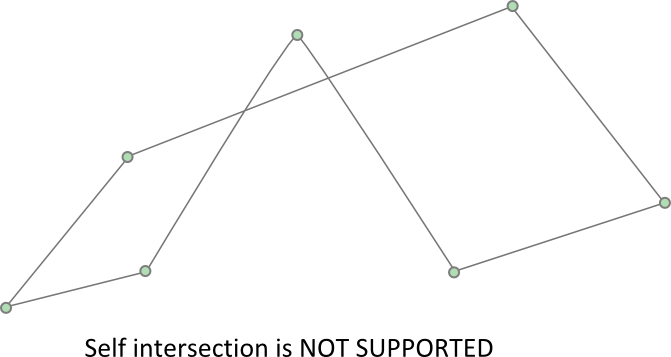
Self-intersection of chain shapes is not supported. It might work, it might not. The code that prevents ghost collisions assumes there are no self-intersections of the chain. Also, very close vertices can cause problems. Make sure all your edges are longer than b2_linearSlop (5mm).

Each edge in the chain is treated as a child shape and can be accessed by index. When a chain shape is connected to a body, each edge gets its own bounding box in the broad-phase collision tree.

   // Visit each child edge.
   for (int32 i = 0; i < chain.GetChildCount(); ++i)
   {
      b2EdgeShape edge;
      chain.GetChildEdge(&edge, i);
      …
   }

Unary Geometric Queries

You can perform a couple of geometric queries on a single shape.

Shape Point Test

You can test a point for overlap with a shape. You provide a transform for the shape and a world point.

   b2Transfrom transform;
   transform.SetIdentity();
   b2Vec2 point(5.0f, 2.0f);
   bool hit = shape->TestPoint(transform, point);

Edge and chain shapes always return false, even if the chain is a loop.

Shape Ray Cast

You can cast a ray at a shape to get the point of first intersection and normal vector. No hit will register if the ray starts inside the shape. A child index is included for chain shapes because the ray cast will only check a single edge at a time.

   b2Transfrom transform;
   transform.SetIdentity();
   b2RayCastInput input;
   input.p1.Set(0.0f, 0.0f, 0.0f);
   input.p2.Set(1.0f, 0.0f, 0.0f);
   input.maxFraction = 1.0f;
   int32 childIndex = 0;
   b2RayCastOutput output;
   bool hit = shape->RayCast(&output, input, transform, childIndex);
   if (hit)
   {
      b2Vec2 hitPoint = input.p1 + output.fraction * (input.p2 – input.p1);
      …
   }

Binary Functions

The Collision module contains bilateral functions that take a pair of shapes and compute some results. These include:

• Overlap
• Contact manifolds
• Distance
• Time of impact

Overlap

You can test two shapes for overlap using this function:

   b2Transform xfA = …, xfB = …;
   bool overlap = b2TestOverlap(shapeA, indexA, shapeB, indexB, xfA, xfB);

Again you must provide child indices to for the case of chain shapes.

Contact Manifolds

LiquidFun has functions to compute contact points for overlapping shapes. If we consider circle-circle or circle-polygon, we can only get one contact point and normal. In the case of polygon-polygon we can get two points. These points share the same normal vector so LiquidFun groups them into a manifold structure. The contact solver takes advantage of this to improve stacking stability.

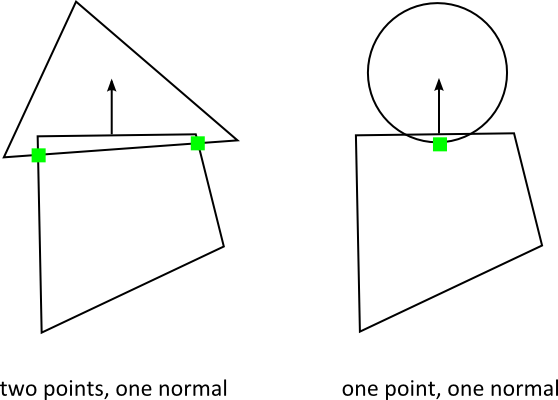
Normally you don’t need to compute contact manifolds directly, however you will likely use the results produced in the simulation.

The b2Manifold structure holds a normal vector and up to two contact points. The normal and points are held in local coordinates. As a convenience for the contact solver, each point stores the normal and tangential (friction) impulses.

The data stored in b2Manifold is optimized for internal use. If you need this data, it is usually best to use the b2WorldManifold structure to generate the world coordinates of the contact normal and points. You need to provide a b2Manifold and the shape transforms and radii.

   b2WorldManifold worldManifold;
   worldManifold.Initialize(&manifold, transformA, shapeA.m_radius, transformB, shapeB.m_radius);
   for (int32 i = 0; i < manifold.pointCount; ++i)
   {
      b2Vec2 point = worldManifold.points[i];
      …
   }

Notice that the world manifold uses the point count from the original manifold.

During simulation shapes may move and the manifolds may change. Points may be added or removed. You can detect this using b2GetPointStates.

   b2PointState state1[2], state2[2];
   b2GetPointStates(state1, state2, &manifold1, &manifold2);
   if (state1[0] == b2_removeState)
   {
      // process event
   }

Distance

The b2Distance function can be used to compute the distance between two shapes. The distance function needs both shapes to be converted into a b2DistanceProxy. There is also some caching used to warm start the distance function for repeated calls. You can see the details in b2Distance.h.

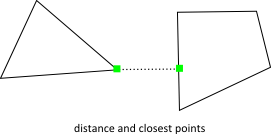
Time of Impact

If two shapes are moving fast, they may tunnel through each other in a single time step.

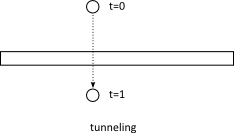
The b2TimeOfImpact function is used to determine the time when two moving shapes collide. This is called the *time of impact *(TOI). The main purpose of b2TimeOfImpact is for tunnel prevention. In particular, it is designed to prevent moving objects from tunneling outside of static level geometry.

This function accounts for rotation and translation of both shapes, however if the rotations are large enough, then the function may miss a collision. However the function will still report a non-overlapped time and will capture all translational collisions.

The time of impact function identities an initial separating axis and ensures the shapes do not cross on that axis. This might miss collisions that are clear at the final positions. While this approach may miss some collisions, it is very fast and adequate for tunnel prevention.

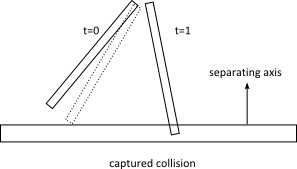
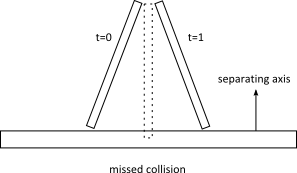
It is difficult to put a restriction on the rotation magnitude. There may be cases where collisions are missed for small rotations. Normally, these missed rotational collisions should not harm game play. They tend to be glancing collisions.

The function requires two shapes (converted to b2DistanceProxy) and two b2Sweep structures. The sweep structure defines the initial and final transforms of the shapes.

You can use fixed rotations to perform a shape cast. In this case, the time of impact function will not miss any collisions.

Dynamic Tree

The b2DynamicTree class is used by LiquidFun to organize large numbers of shapes efficiently. The class does not know about shapes. Instead it operates on axis-aligned bounding boxes (AABBs) with user data pointers.

The dynamic tree is a hierarchical AABB tree. Each internal node in the tree has two children. A leaf node is a single user AABB. The tree uses rotations to keep the tree balanced, even in the case of degenerate input.

The tree structure allows for efficient ray casts and region queries. For example, you may have hundreds of shapes in your scene. You could perform a ray cast against the scene in a brute force manner by ray casting each shape. This would be inefficient because it does not take advantage of shapes being spread out. Instead, you can maintain a dynamic tree and perform ray casts against the tree. This traverses the ray through the tree skipping large numbers of shapes.

A region query uses the tree to find all leaf AABBs that overlap a query AABB. This is faster than a brute force approach because many shapes can be skipped.

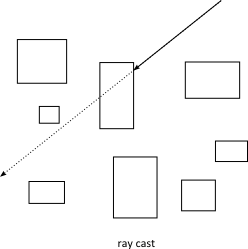
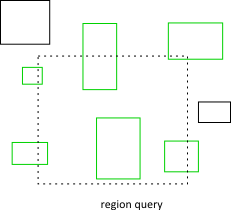
Normally you will not use the dynamic tree directly. Rather you will go through the b2World class for ray casts and region queries. If you plan to instantiate your own dynamic tree, you can learn how to use it by looking at how LiquidFun uses it.

Broad-phase

Collision processing in a physics step can be divided into narrow-phase and broad-phase. In the narrow-phase we compute contact points between pairs of shapes. Imagine we have N shapes. Using brute force, we would need to perform the narrow-phase for N*N/2 pairs.

The b2BroadPhase class reduces this load by using a dynamic tree for pair management. This greatly reduces the number of narrow-phase calls.

Normally you do not interact with the broad-phase directly. Instead, LiquidFun creates and manages a broad-phase internally. Also, b2BroadPhase is designed with LiquidFun’s simulation loop in mind, so it is likely not suited for other use cases.

This content is licensed under Creative Commons Attribution 4.0. For details and restrictions, please see the Content License.