Figure 1: Miipher2 Architecture
Figure 2: ReverbMiipher Architecture (Proposed)
Reverberation encodes spatial information regarding the acoustic source environment, yet traditional Speech Restoration (SR) usually completely removes reverberation. We propose ReverbMiipher, an SR model extending parametric resynthesis framework, designed to denoise speech while preserving and enabling control over reverberation. ReverbMiipher incorporates a dedicated ReverbEncoder to extract a reverb feature vector from noisy input. This feature conditions a vocoder to reconstruct the speech signal, removing noise while retaining the original reverberation characteristics. A stochastic zero-vector replacement strategy during training ensures the feature specifically encodes reverberation, disentangling it from other speech attributes. This learned representation facilitates reverberation control via techniques such as interpolation between features, replacement with features from other utterances, or sampling from a latent space. Objective and subjective evaluations confirm ReverbMiipher effectively preserves reverberation, removes other artifacts, and outperforms the conventional two-stage SR and convolving simulated room impulse response approach. We further demonstrate its ability to generate novel reverberation effects through feature manipulation.
Figure 1: Miipher2 Architecture
Figure 2: ReverbMiipher Architecture (Proposed)
The proposed method, ReverbMiipher, is an extended model of Miipher-2 endowed with reverberation controllability as shown in Figure 2. This model incorporates an additional feature extraction module termed ReverbEncoder $\mathcal{R}$. The ReverbEncoder takes a log-mel spectrogram extracted from $\bm{x}$ and outputs a reverb-feature $\bm{c} = \mathcal{R}(\bm{x}) \in \mathbb{R}^{D}$, which is a vector embedded with reverberation characteristics. Here, $D=512$ is the dimension of reverb-feature. By utilizing $\bm{c}$ as an additional conditioning for $\mathcal{V}$, ReverbMiipher outputs a signal in which only reverberation is preserved and all other artifacts are removed as $\mathcal{V}(\hat{\bm{h}}_{s}, \bm{c})$. Furthermore, applying control to $\bm{c}$ enables the manipulation of reverberation.
This page presents audio samples for our paper. Spectrograms for each audio can be clicked to zoom.
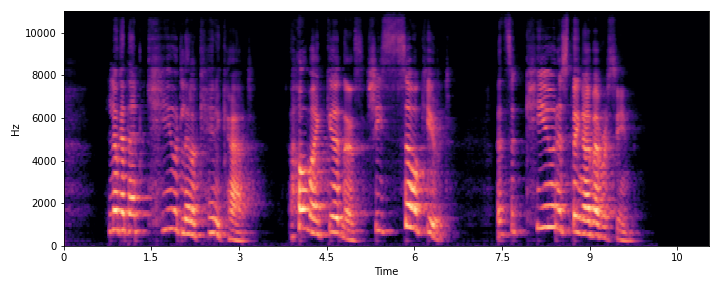
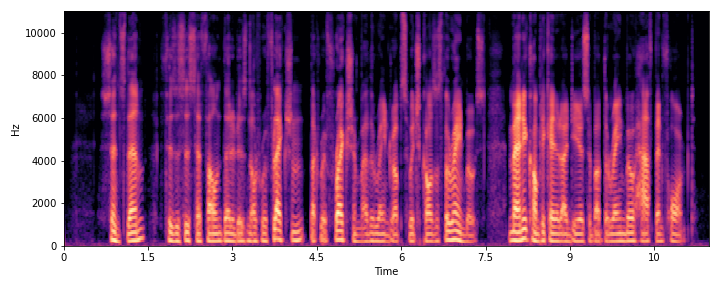
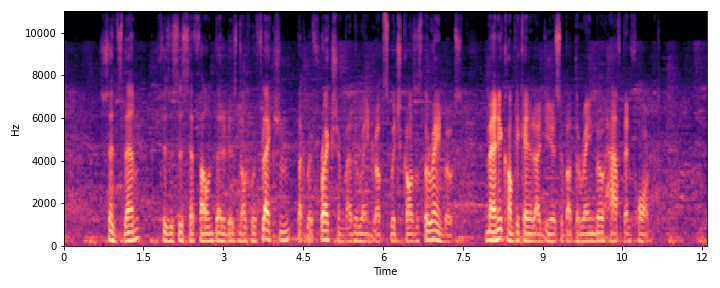
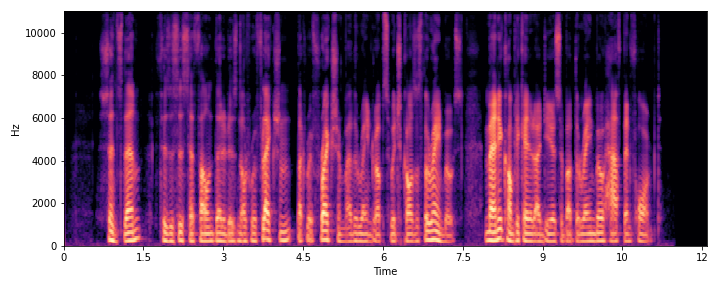
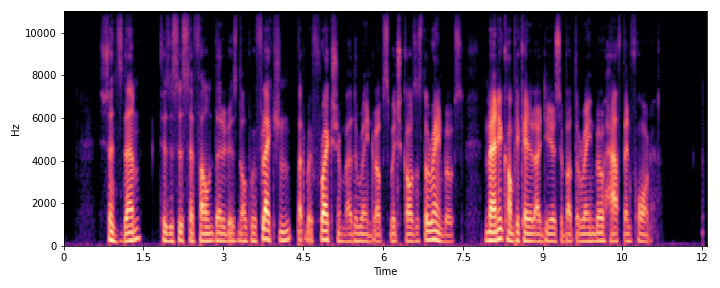
This section demonstrates the model's ability to remove noise while preserving the original reverberation characteristics of the speech signal. Compare the "Ground truth reverb" with the "ReverbMiipher (Proposed)" output.
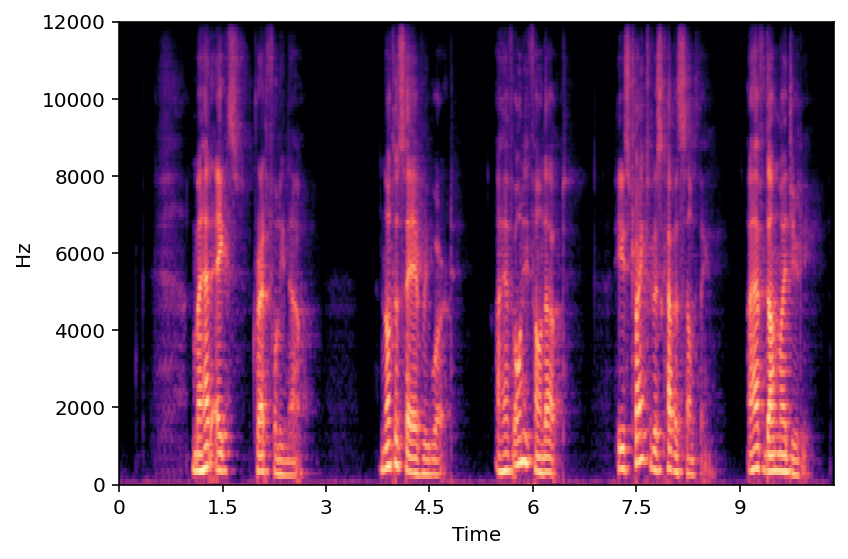
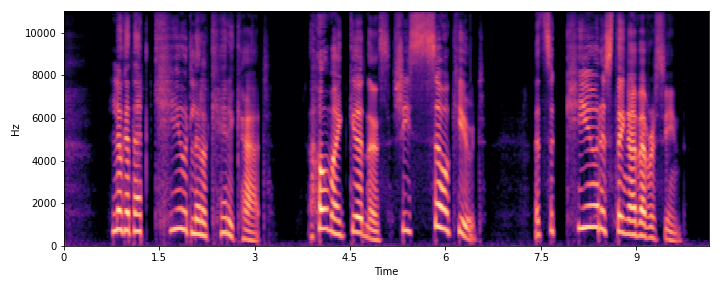
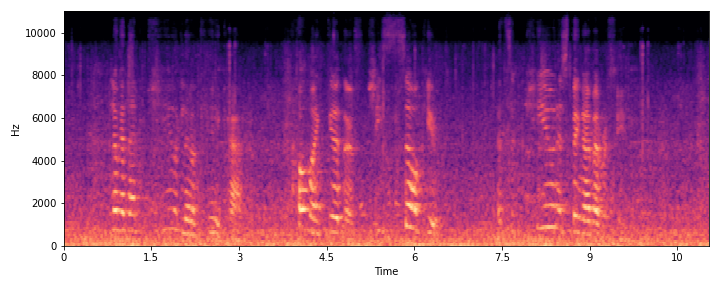
| Sample Index | Clean | Noisy | Ground Truth Reverb | Miipher-2 | Miipher-RIR | ReverbMiipher (Proposed) |
|---|---|---|---|---|---|---|
| S0 |
|
|
|
|
|
|
| S1 |
|
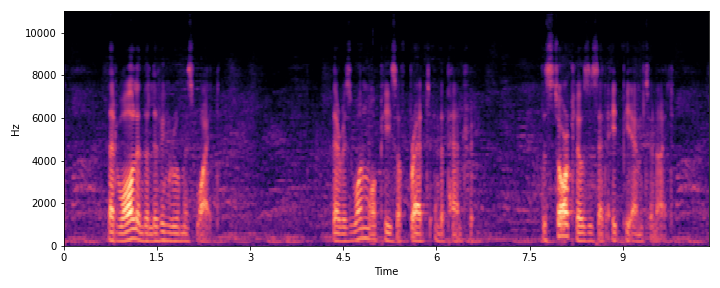
|
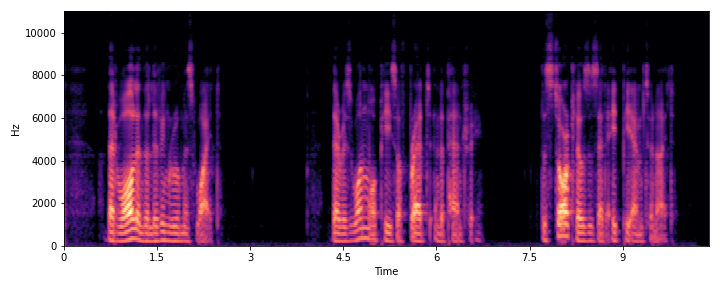
|
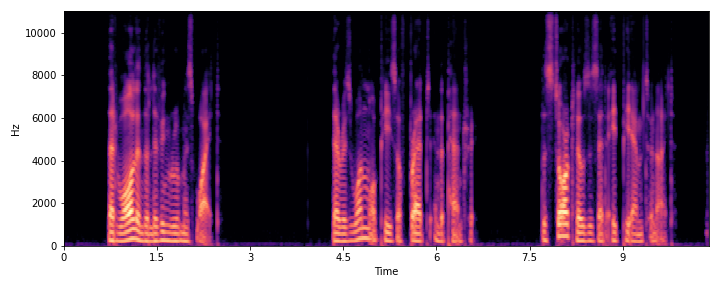
|
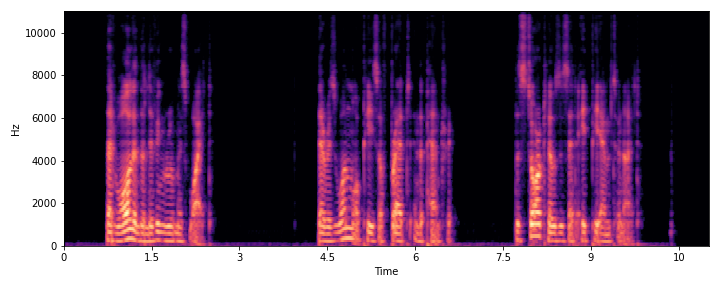
|

|
| S2 |

|
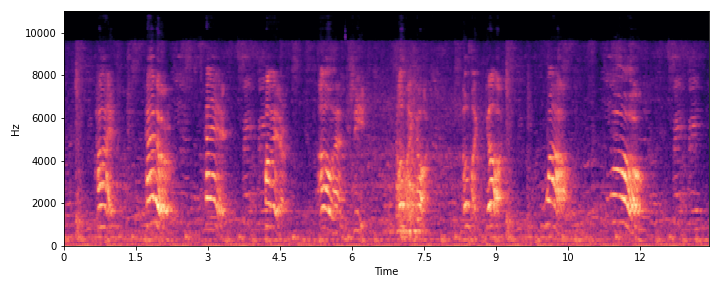
|

|
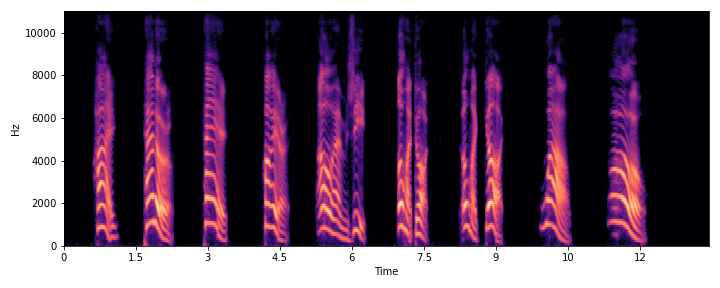
|
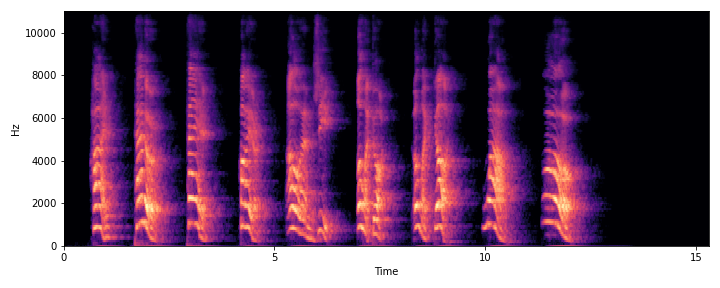
|
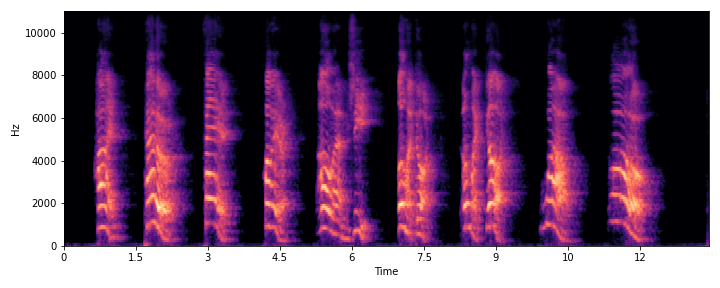
|
| S3 |

|
|
|
|
|

|
| S4 |
|
|
|
|
|
|
| S5 |
|
|
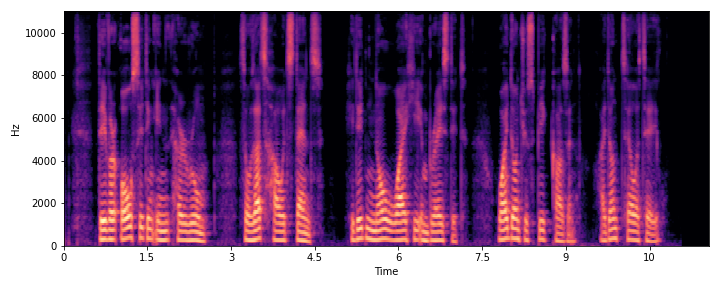
|

|
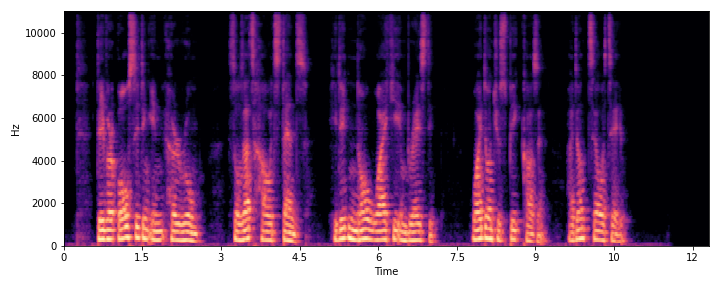
|
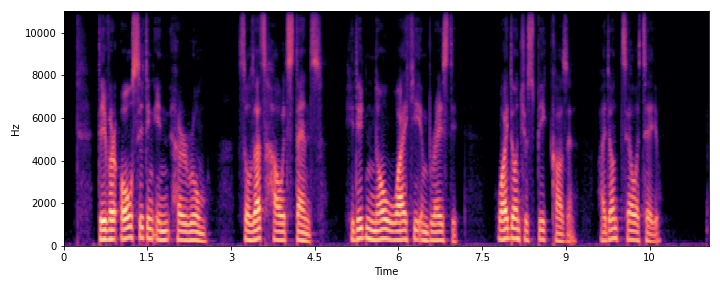
|
Use the slider to adjust the α for the linear interpolation. The spectrogram and audio will update dynamically. An α of 1.0 corresponds to the reverberant speech, while 0.0 is for a drier signal.
The linear interpolation can be expressed as $ \bm{c}(\alpha) = (1-\alpha) \bm{c}_1 + \alpha \bm{c}_2,\text{for } 0 \leq \alpha \leq 1 $.
In this example, $c_1$ corresponds to the reverb feature extracted from dry signal while $c_0$ corresponds to the reverberant signal
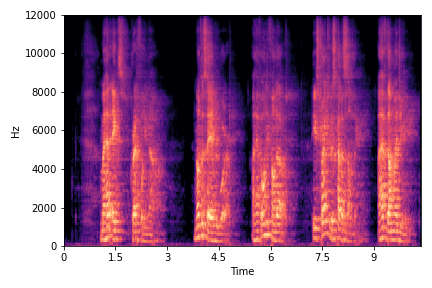
This section showcases results from sampling different reverb features from 2D plane acquired in PCA. The visualization of reverb feature with respect to RT60 and DRR are shown below. We have picked 3 samples each having different reverberation characteristics.
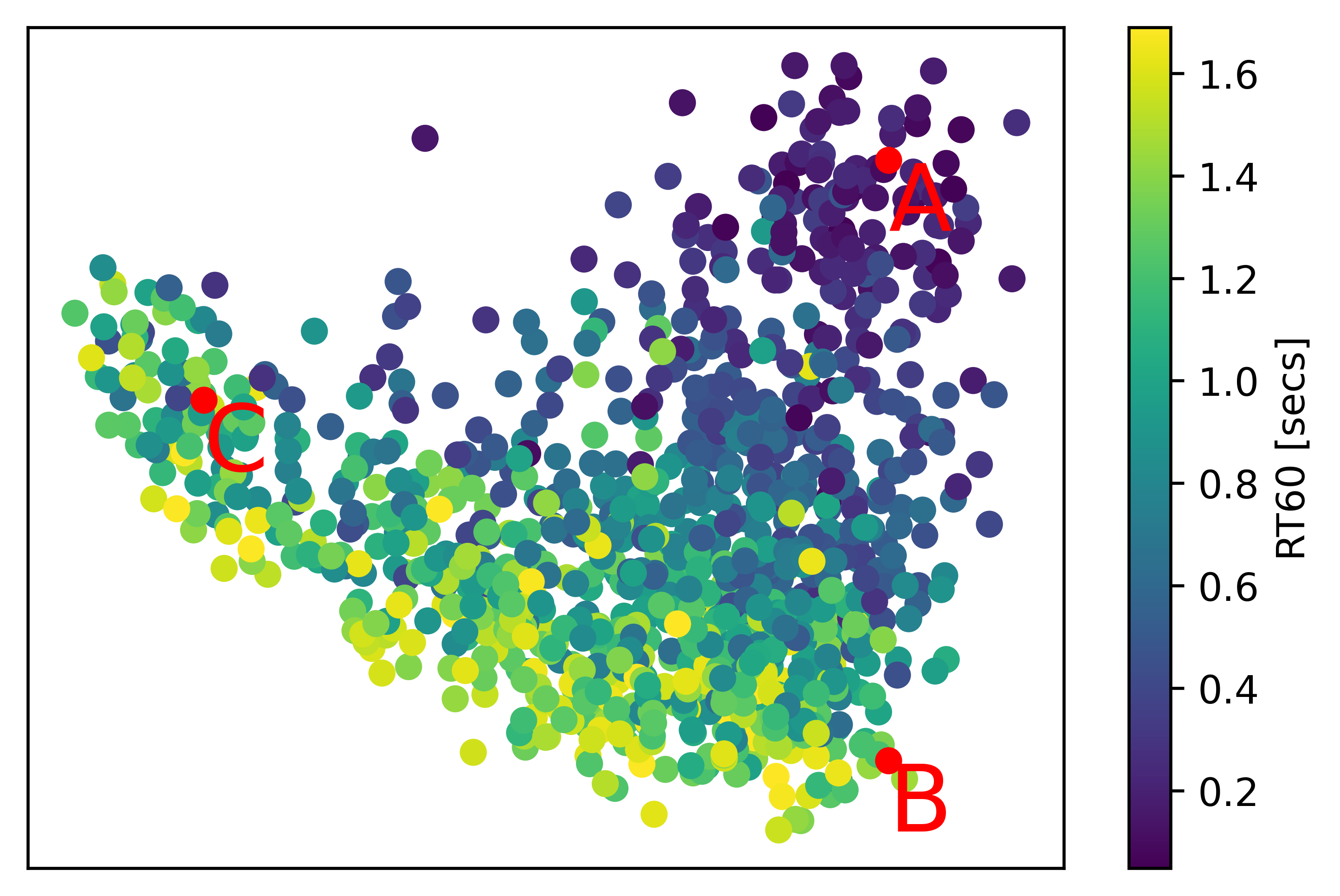
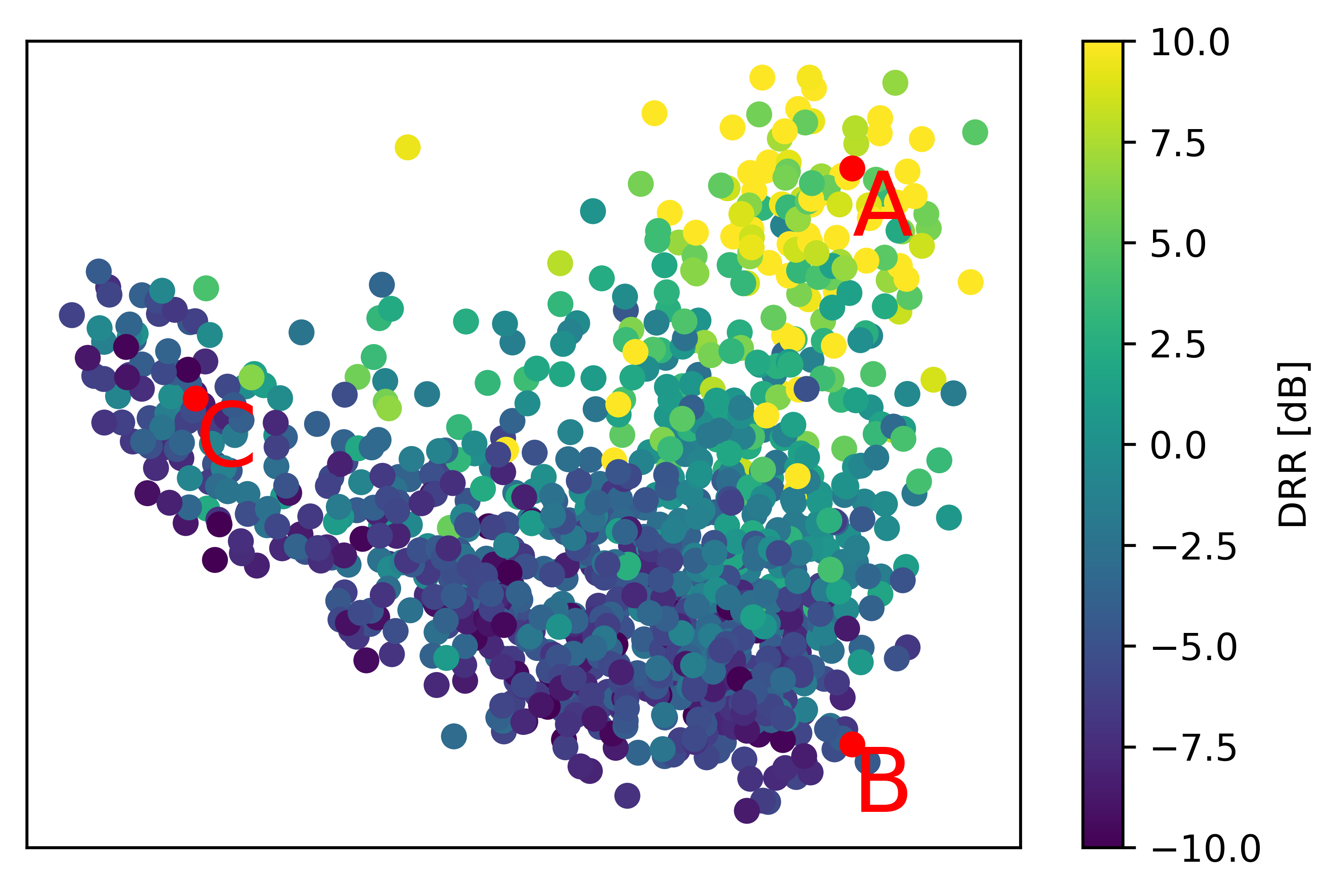
Sample A

Sample B

Sample C