Dimension-Order Topology Types

Overview

The dimension-order topology is a topology where the arrangement of the routers are described by their location in a dimensional space. The topology has a hierarchical structure where dimension n is composed of structures from dimension n-1. One or more endpoint nodes are connected to a router.

k-ary n-cube

A k-ary n-cube topology consists of kⁿ routers arranged in an n-dimensional cube with k routers along each dimension. Each router is assigned an n-digit radix-k address {a_n−1, ..., a₀} and is connected to all routers with addresses that differ by ±1(mod k) in exactly one address digit. Each dimension is constructed using k k-ary (n-1)-cubes. The channels between the routers can be unidirectional or bidirectional. In practice, the channels are bidirectional.

Ring Topology

Figure Ring_4ary_1cube_example. A ring topology with four routers, also known as a 4-ary 1-cube topology.

The ring topology is a special instance of the k-ary n-cube, where n is equal to one. Figure Ring_4ary_1cube_example shows a ring topology with four routers, also known as a 4-ary 1-cube topology. The dotted lines show the connectivity between routers 0 and k-1 for a dimension.

Symmetric Torus Topology

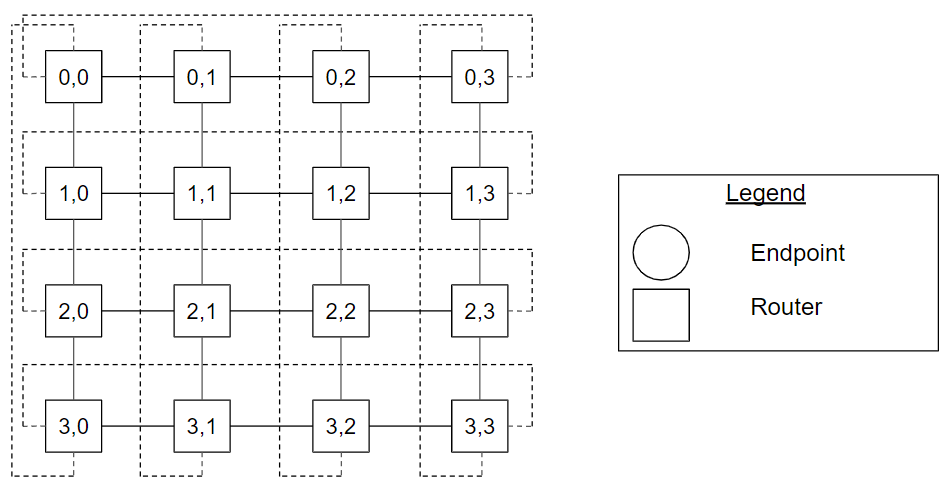
Figure Symmetric_Torus_4ary_2cube_example. A symmetric torus topology with four routers along each dimension, also known as a 4-ary 2-cube topology.

The symmetric torus topology is a special instance of the k-ary n-cube, where n is equal to two. Figure Symmetric_Torus_4ary_2cube_example shows a symmetric torus topology with four routers along each dimension, also known as a 4-ary 2-cube topology. Router (3,0) has address 3 in a dimension and 0 in the other dimension. The dotted lines show the connectivity between routers 0 and k-1 for a dimension.

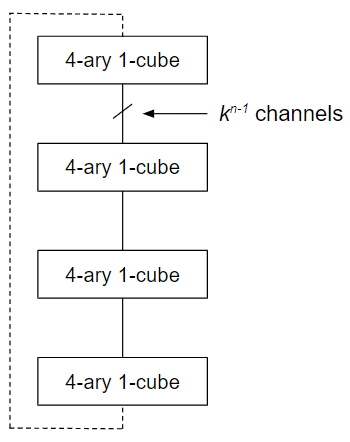
Figure 4ary_2cube_construction_example. The construction of a symmetric torus (4-ary 2-cube) topology using 4-ary 1-cubes.

Figure 4ary_2cube_construction_example shows the construction of a symmetric torus (4-ary 2-cube) topology using 4-ary 1-cubes (ring topologies).

multi-radix n-cube

A multi-radix n-cube is a generalized form of a k-ary n-cube topology where the radix (number of router nodes) for each dimension is explicitly stated. Each router is assigned an n-digit where the digit at index i has the radix of dimension i. A 2,3-ary 2-cube describes a grid-like topology with a radix of 2 in one dimension and radix of 3 in the other dimension.

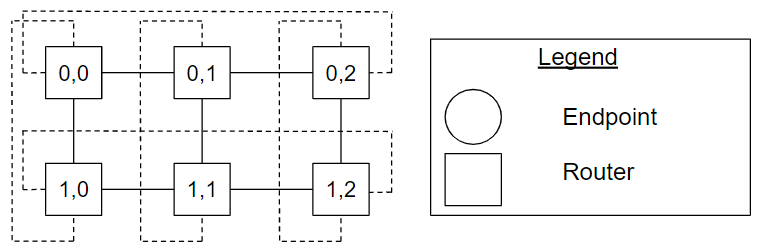
Figure 2,3-ary_2cube_example. A 2,3-ary 2-cube topology example.

Figure 2,3-ary_2cube_example shows a 2,3-ary 2-cube topology example. The dotted lines show the connectivity between router 0 and router radix_i - 1 for each dimension.

k-ary n-mesh

A k-ary n-mesh is a k-ary n-cube topology with the connection from address a_k−1 to address a₀ omitted in each dimension.

Line

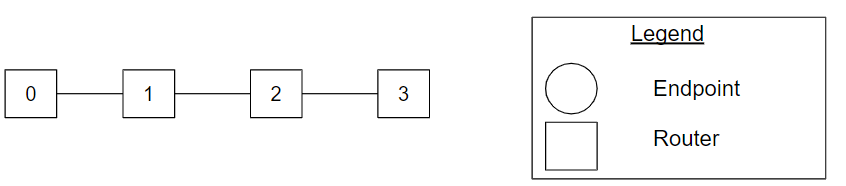
Figure Line_4ary_1mesh_example. A line topology with four routers, also known as a 4-ary 1-mesh topology.

The line topology is a special instance of the k-ary n-mesh, where n is equal to one. Figure Line_4ary_1mesh_example shows a line topology with four routers, also known as a 4-ary 1-mesh topology. Compared to the ring topology in Figure Ring_4ary_1cube_example, the connection from router 0 to router 3 is omitted.

Symmetric Mesh

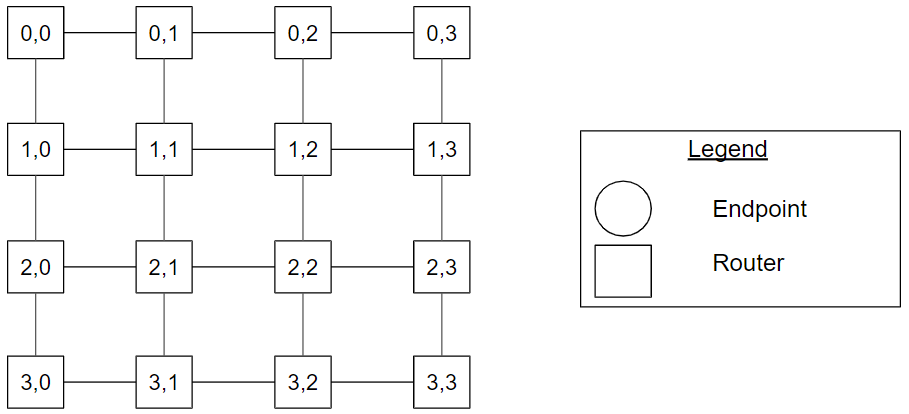
Figure Symmetric_Mesh_4ary_2mesh_example. A symmetric mesh topology with four routers along each dimension, also known as a 4-ary 2-mesh topology.

The symmetric torus mesh is a special instance of the k-ary n-mesh, where n is equal to two. Figure Symmetric_Mesh_4ary_2mesh_example shows a symmetric mesh topology with four routers along each dimension, also known as a 4-ary 2-mesh topology. Router (1,2) has address 1 in a dimension and 2 in the other dimension. Compared to the torus topology in Figure Symmetric_Torus_4ary_2cube_example, the connections between the pair of routers [(0,0), (0,3)], [(1,0), (1,3)], [(2,0), (2,3)], [(3,0), (3,3)], [(0,0), (3,0)], [(0,1), (3,1)], [(0,2), (3,2)], and [(0,3), (3,3)] are omitted.

multi-radix n-mesh

Similar to the multi-radix n-cube, a multi-radix n-mesh is a generalized form of a k-ary n-mesh topology where the radix (number of router nodes) for each dimension is explicitly stated. Each router is assigned an n-digit where the digit at index i has the radix of dimension i. A 2,3-ary 2-mesh describes a grid-like topology with a radix of 2 in one dimension and radix of 3 in the other dimension.

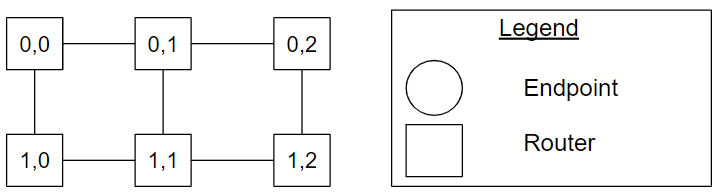
Figure 2,3-ary_2mesh_example. A 2,3-ary 2-mesh topology example.

Figure 2,3-ary_2mesh_example shows a 2,3-ary 2-mesh topology example. Compared to the multi-radix n-cube topology in Figure 2,3-ary_2cube_example, the connections from the pair of routers [(0,0), (0,2)], [(1,0), (1,2)], [(0,0), (1,0)], [(0,1), (1,1)] and [(0,2), (1,2)] are omitted.

Cheat Sheet

• A k-ary n-cube topology consists of kⁿ routers arranged in an n-dimensional cube with k router nodes along each dimension. Each router is assigned an n-digit radix-k address {a_n−1, ..., a₀} and is connected to all routers with addresses that differ by ±1 (mod k) in exactly one address digit. Each dimension is constructed using k k-ary (n-1)-cubes where there are k routers in the first dimension.
• A multi-radix n-cube is a generalized form of a k-ary n-cube topology where the radix (number of routers) for each dimension is explicitly stated. Each router is assigned an n-digit where the digit at index i has the radix of dimension i.
• A k-ary n-mesh is a k-ary n-cube topology with the connection from address a_k−1 to address a₀ omitted in each dimension.
• Similar to the multi-radix n-cube, a multi-radix n-mesh is a generalized form of a k-ary n-mesh topology where the radix (number of routers) for each dimension is explicitly stated. Each router is assigned an n-digit where the digit at index i has the radix of dimension i.
• Channel direction can be unidirectional or bidirectional.
• Ring: k-ary 1-cube
• Symmetric Torus: k-ary 2-cube
• Line: k-ary 1-mesh
• Symmetric Mesh: k-ary 2-mesh

References

William James Dally and Brian Patrick Towles. 2004. Principles and Practices of Interconnection Networks. Morgan Kaufmann Publishers Inc., San Francisco, CA, USA.